SRSG UNIVERSE-HPC Training

YouTube lecture recording from October 2020

The following YouTube video was recorded for the 2020 iteration of the course. The material is still very similar:

Complex Numbers

Imaginary numbers

The Imaginary Number $i$ :

The polynomial $~~x^2-1=0~~$ has two real roots: $~~1~~$ and $~~-1~~$
The polynomial $~~x^2+1=0~~$ has no real roots.

Consider solving: $x^2 = 1\qquad{\rm and}\qquad x^2 = -1$

We introduce an "imaginary" number $~~i~~$ so that there are two solutions to $~~x^2 = -1~~$ : $~~i~~$ and $~~-i~~$ . That is, $~~i~~$ is a number with the property that $~~i^2=-1$ .

Complex numbers

The complex numbers are the set of all expressions of the form $a + bi$ where $i^2=-1$ and $a$ and $b$ are real numbers:

$\mathbb{C}=\left\{a + bi~~\vert~~a,~b~\in\mathbb{R}\right\}$

For $z=a+bi\in\mathbb{C}$ we define the real and imaginary parts of $z$ to be ${\Re}(z) = a$ and $\Im(z)=b$ .

The imaginary number $i$ has no home on the real number line. Instead, we locate it on the complex plane at the point $(0,1)$ .

we can represent any complex number $z=a+bi$ as the point $(a,b)$ in the complex plane.
The coordinates $(a,b)$ are usually called the cartesian coordinates for $z$ . (Named after the mathematician and philosopher Rene Descartes).
In this plane, the real numbers lie on the horizontal axis. We usually refer to the horizontal axis of $\mathbb{C}$ as the real axis.

The following plot shows a complex number with a real component of 18 and an imaginary component of 12:

The complex plane

Complex conjugates

The complex plane $\mathbb{C}$ contains all of the roots of every polynomial.

E.g., let's look at a quadratic equation. Recall the quadratic formula:

$ax^2 +bx +c \iff x= {-b \pm\sqrt{b^2-4ac}\over 2a}$

Now, let's consider this specific quadratic equation:

$x^2-8x+25 = 0$

which we can solve using the quadratic formula:

$={{8\pm\sqrt{64-100}}\over2}={{8\pm\sqrt{-36}}\over2}={{8\pm6i}\over2}=4\pm3i$

Note that these two roots are reflections of one another through the real axis. They are conjugates of one another.
In general, let $z=a + bi$ . The conjugate of $z$ is the complex number $\bar{z}=a-bi$ .

We can also use Sympy's solve method to solve polynomials:

import sympy as sp
x = sp.symbols('x')
sp.solve(x**2 - 8*x + 25)

$\displaystyle \left[ 4 - 3 i, \ 4 + 3 i\right]$

Modulus (size) of a complex number

The distance to a point on the complex plane from 0 is called its modulus, and we find this by calculating the hypotenuse of the triangle with base ${\Re}(z)$ and height $\Im(z)$ :

E.g. The modulus of $4\pm3i$ is $\sqrt{3^2+4^2}=\sqrt{9+16}=\sqrt{25}=5$

In general, the modulus of $z=a+bi$ is the real number $|z|=\sqrt{a^2+b^2}$ .
The modulus is connected to the conjugate by means of the formula $z\cdot \bar{z}=|z|^2$ . Indeed:

\begin{align} z\cdot\bar{z}&=(a+bi)(a-bi)=a^2-(bi)^2=a^2-b^2\cdot i^2\\ &=a^2-b^2(-1)=a^2+b^2=|z|^2 \end{align}

Complex numbers in Python

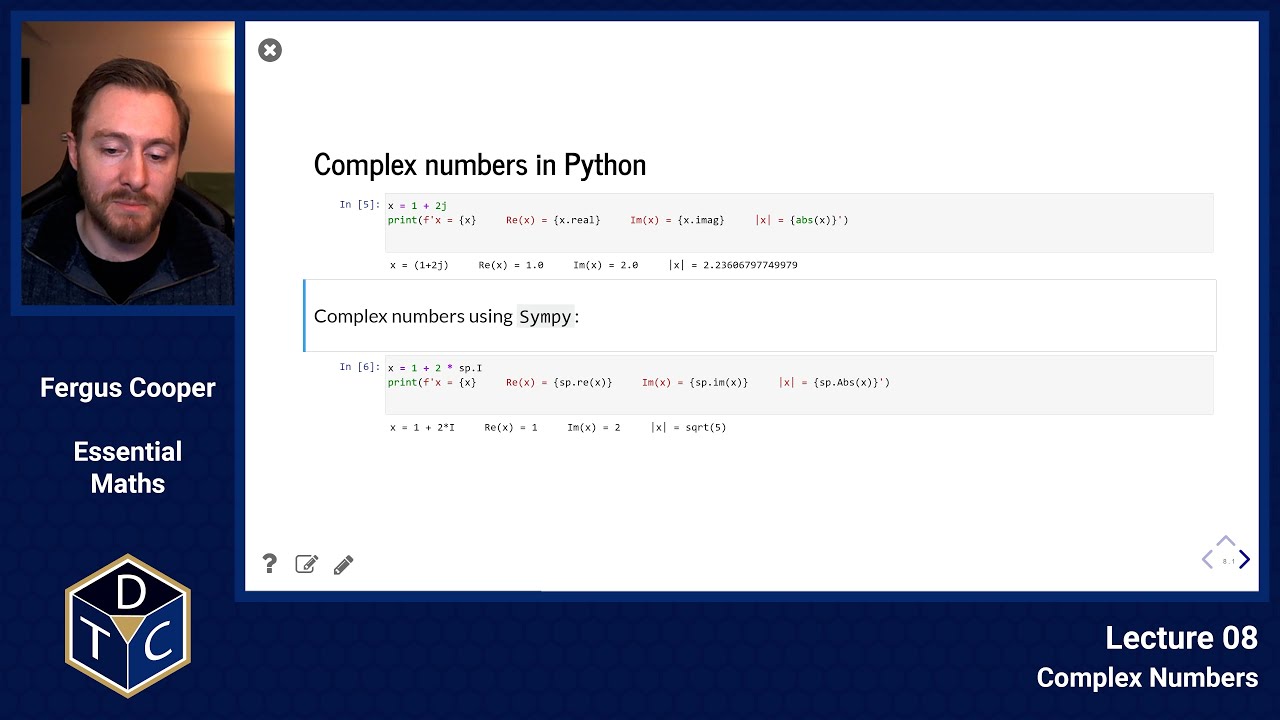
Note that, in Python, because i is often used as an index variable in loops, the language uses j, instead, to represent the imaginary unit:

x = 1 + 2j
print(f'x = {x}     Re(x) = {x.real}     Im(x) = {x.imag}     |x| = {abs(x)}')

x = (1+2j)     Re(x) = 1.0     Im(x) = 2.0     |x| = 2.23606797749979

In Sympy, the imaginary unit is sp.I:

x = 1 + 2 * sp.I
print(f'x = {x}     Re(x) = {sp.re(x)}     Im(x) = {sp.im(x)}     |x| = {sp.Abs(x)}')

x = 1 + 2*I     Re(x) = 1     Im(x) = 2     |x| = sqrt(5)

Addition and Subtraction

Addition and subtraction of complex numbers work as you would expect:

$(a+bi)\pm(c+di)=(a\pm c) + (b\pm d)i$

and

$-(a+bi)=-a-bi$

Try adding: $(5+6i)+(1-i)$ :

print((5 + 6j) + (1 - 1j))

(6+5j)

Try subtracting: $(5+6i)-(1-i)$ :

print((5 + 6j) - (1 - 1j))

(4+7j)

Multiplication

Multiplication is not quite so convenient in cartesian coordinates:

\begin{align*} (a+bi)(c+di)&=ac + adi + bci + bidi \\ &= ac + adi + bci -bd \\ &= (ac-bd)+(ad+bc)i \end{align*}

Try multiplying: $(5+6i)(1-i)$ :

print((5 + 6j) * (1 - 1j))

(11+1j)

Division

Division is even more awkward in cartesian coordinates: we have to multiply the numerator and the denominator by the complex conjugate of the denominator.

\begin{align*} {{a+bi}\over{c+di}}&={{(a+bi)(c-di)}\over{(c+di)(c-di)}}\\ &={{(ac+bd)+(bc-ad)i}\over{c^2+d^2}}=\left({{ac+bd}\over{c^2+d^2}}\right)+ \left({{bc-ad}\over{c^2+d^2}}\right)i \end{align*}

Try dividing: ${(-4+7i)\over (2+3i)}$ :

print((-4 + 7*sp.I) / (2 + 3*sp.I))

(-4 + 7*I)*(2 - 3*I)/13

Polar Coordinates

It is often convenient to represent the complex number $z = a + bi$ in terms of its polar coordinates $\langle r,\theta\rangle$ .

The angle $\theta$ is called the argument of $z$ .
The real number $r=|z|$ is sometimes denoted mod $(z)$ .

Representing a complex number in polar coordinates

Connection between cartesian and polar

Let $z=x+iy$ . If we are given the polar coordinates of $z$ and want to express the cartesian coordinates use

$x=r\cos\theta$ > $y=r\sin\theta$ > $z=r\cos\theta + ri\sin\theta=r(\cos\theta + i\sin\theta)$

If we are given the cartesian coordinates and want to find the polar coordinates, use:

r={\rm mod}(z)=|z|=\sqrt{x^2+y^2}

\begin{align*} \theta={\rm arg}(z)=\tan^{-1}{y\over x}= \begin{cases}\pi/2,&{\rm ~if~}~~ x=0,y>0 \\ -\pi/2,&{\rm ~if~}~~ x=0,y<0 \\ \arctan\left({y\over x}\right),&{\rm ~if~}~~ x>0\\ \arctan\left({y\over x}\right)+\pi,&{\rm ~if~}~~ x<0, y\geq 0\\ \arctan\left({y\over x}\right)-\pi,&{\rm ~if~}~~ x<0, y<0\\ \end{cases} \end{align*}

Not: all of the fuss about the value of $\theta$ in the formula above is to make sure that $z$ gets into the proper quadrant. Beware of the sign of this tangent: it depends on which quadrant you are in.

The positive $x$ axis is defined as having $\theta=0$ and positive $\theta$ goes in an anticlockwise sense around the $x-y$ plane.

Some examples

1

Find the cartesian coordinates for the complex number $z$ with polar coordinates $r=2$ and $\theta=\pi/6$ .

$\Re(z)=x=r\cos\theta=2\cos(\pi/6)=2\left({{\sqrt{3}\over2}}\right)=\sqrt{3}$ > $\Im(z)=y=r\sin\theta=2\sin(\pi/6)=2\left({{1\over2}}\right)=1$

Therefore, $z = \sqrt{3} + i$ .

import cmath
import numpy as np
print(cmath.rect(2, np.pi/6))

(1.7320508075688774+0.9999999999999999j)

2

Find the polar coordinates for the complex number $z= -3+4i$ .

$|z|=r =$ $\sqrt{(-3)^2+4^2}=\sqrt{25}=5$ ${\rm arg}(z)=\theta=\arctan\left({{y}\over{x}}\right)=$ $-0.93+\pi{\rm ~radians}\approx 127^\circ$

print(cmath.polar(-3 + 4j))

(5.0, 2.214297435588181)

3

Find the polar coordinates for the complex number $z= -2i$ .

${\rm mod}(z)=r = |z|=2$ > ${\rm arg}(z)=\theta=-{{\pi}\over2}$

print(cmath.polar(-2j))

(2.0, -1.5707963267948966)

Multiplication in Polar Coordinates

First a reminder of three useful and important identities:

$\cos^2\theta + \sin^2\theta = 1$ > $\cos(\theta_1+\theta_2)=\cos\theta_1\cos \theta_2 - \sin\theta_1\sin\theta_2$ > $\sin(\theta_1+\theta_2)=\sin\theta_1\cos \theta_2 + \sin\theta_2\cos\theta_1$

Now, let $z_1=r_1\cos\theta_1+ir_1\sin\theta_1$ and $z_2=r_2\cos\theta_2+ir_2\sin\theta_2$ .

We first compute the real part of the product $z_1\cdot z_2$ :

\begin{align*} \Re(z_1\cdot z_2) &= r_1\cos\theta_1\cdot r_2\cos\theta_2 - r_1\sin\theta_1\cdot r_2\sin\theta_2\cr &=r_1r_2(\cos\theta_1\cos\theta_2 - \sin\theta_1\sin\theta_2)\cr &=r_1r_2\cos(\theta_1 + \theta_2) \end{align*}

Note that for the real part the moduli have been multiplied and the arguments added.

Now we compute the imaginary part of $z_1\cdot z_2$ :

\begin{align*} \Im(z_1\cdot z_2) &= r_1\sin\theta_1\cdot r_2\cos\theta_2 + r_2\sin\theta_2\cdot r_1\cos\theta_1\cr &=r_1r_2(\sin\theta_1\cos\theta_2 - \sin\theta_2\cos\theta_1)\cr &=r_1r_2\sin(\theta_1 + \theta_2) \end{align*}

For the imaginary part too, the moduli multiply while the arguments add.

This gives a relatively compact and highly geometric result for the product:

$z_1\cdot z_2 = r_1r_2(\cos(\theta_1 + \theta_2)+i\sin(\theta_1 + \theta_2))$

It is multiplicative in the modulus and additive in the argument:

$|z_1z_2|= |z_1\cdot |z_2|$ > $\arg(z_1z_2)=\arg (z_1)+ \arg( z_2)$

This means that when we multiply by $z$ , we are rotating through the angle $\arg(z)$ and radially stretching by a factor of $|z|$ .

A Remarkable Connection with $e^{i\theta}$

First, think of $z=\cos\theta + i\sin\theta$ as a function of $\theta$ and differentiate with respect to $\theta$ :

${\rm~~(1)~~~~}\frac{{\rm d}z}{{\rm d}\theta}=\frac{{\rm d}}{{\rm d}\theta}\left(\cos\theta+i\sin\theta\right)=-\sin\theta+i\cos\theta$

Next notice that the right-hand side is just the product $iz$ :

${\rm~~(2)~~~~}iz=i(\cos\theta+i\sin\theta)=i\cos\theta+i^2\sin\theta=-\sin\theta+i\cos\theta$

Thus, from (1) and (2), $\frac{{\rm d}z}{{\rm d}\theta}=iz$

This is a separable differential equation (which we will cover properly in the remainder of the course):

$\int{dz\over iz}=\int d\theta~~~~~~~~~\Rightarrow~~~~~~{1\over i}~\ln z =\theta +c~~~~\Rightarrow~~~~\ln z =i\theta +ic$

In exponential form:

$z=e^{i\theta+ic}~~=~~e^{i\theta}~e^{ic}~~=~~Ae^{i\theta}~~~~{\rm~ with}~~~~ A=e^{ic}$

When $\theta=0$ , $z=1$ , giving $A=1$ , so:

$z=\cos\theta + i \sin\theta=e^{i\theta}~~~~~~~~~~~~\rm (3)$

Similarly, we can show that:

$z=\cos\theta - i \sin\theta=e^{-i\theta}~~~~~~~~~~~~\rm (4)$

Adding (3) and (4), and subtracting (3) and (4) gives:

$\cos\theta ={e^{i\theta}+ e^{-i\theta}\over 2}~~~~~~~~~~~~~~~~~~~~~~~~~\sin\theta ={ e^{i\theta}-e^{-i\theta}\over 2i}$

This demonstrates that any complex number can be written:

$z=x+iy=r(\cos\theta + i\sin\theta)=r~e^{i\theta}$

Several important consequences

Any complex number can be written in the polar form $z = re^{i\theta}$ where $r=|z|$ and $\theta=\arg(z)$ .
The unit circle in $\mathbb{C}$ consists exactly of those complex numbers with modulus equal to 1, that is the numbers $e^{i\theta}$ .
Multiplication on the unit circle $r=1$ can be carried out by adding the angles:

$e^{i\theta_1}\cdot e^{i\theta_2} = e^{i(\theta_1+\theta_2)}$ > $z=x+iy=r(\cos\theta + i\sin\theta)=r~e^{i\theta}$
Exponentiation on the unit circle $r=1$ can be done by multiplying the angle by the index:

$\left(e^{i\theta}\right)^n = e^{i\theta n}=e^{i(n\theta)}$
This result is known as DeMoivre's Theorem. It is usually stated in its cartesian form:

$(\cos\theta + i\sin\theta)^n=\cos(n\theta) + i\sin(n\theta)$
Finally, the famous identity by Leonhard Euler

$e^{\pi i}+1=0$

Introductory problems

Introductory problems 1

Simplify:

$\displaystyle 2-2i\quad+\quad 3+i$
$\displaystyle 4-6i\quad+\quad 19+4i$
$\displaystyle (1-i)^2$
$\displaystyle (2+i)^2$
$\displaystyle (4-3i)/(2+6i)$
$\displaystyle (1+2i)/(1-3i)$
$\displaystyle (2-i)^{-2} +(2+i)^{-2}$
$\displaystyle (5-i)^{-2} -(5+i)^{-2}$

Introductory problems 2

Find the sum, difference, product and quotient of the complex numbers $\displaystyle z_1=5+3i$ and $\displaystyle z_2=-4+2i$ .

Main problems

Main problems 1

Solve the following equations for $z$ :

$\displaystyle (7 + i)z - 3i = 6$
$\displaystyle {(z-i)\over (z+i)}={2\over 3}$
$\displaystyle z^2 + (1+4i)z + (15 + 27 i) = 0$

Main problems 2

Represent the complex numbers $\displaystyle z_1= 5-2i$ and $\displaystyle z_2=-2 +4i$ on a sketch/plot of the complex plane (an Argand diagram).

Write down $z_1$ and $z_2$ in polar form (either give $r$ and $\theta$ for each, or write them as exponentials).
What is the product of $z_1$ and $z_2$ ?

Main problems 3

Find the sum, difference, product and quotient of the complex numbers $\displaystyle z_1=5e^{4i}$ and $\displaystyle z_2=3e^{-2i}$ . Can you represent the results on an Argand diagram?

Main problems 4

What are the $\displaystyle (x,y)$ coordinates of the complex number $\displaystyle 5e^{4i}$ ?

Main problems 5

If $\displaystyle z=1+i$ , mark on an Argand diagram the four points $\displaystyle A, B, C {\rm ~and~} D$ representing $\displaystyle z, z^2, z^3 {\rm ~and~} z^4$ respectively.

Find by calculation or from your diagram, the moduli and arguments of the complex numbers $\displaystyle z^2-1$ and $\displaystyle z+z^4$ .

Main problems 6

Find the complex numbers represented by the vertices of a square if one vertex represents $\displaystyle 3+3i$ and the centre of the square represents $\displaystyle 1+2i$ .

Extension problems

Extension problems 1

Experiment with using Python to solve the problems and confirm your pen & paper solutions.

Complex numbers

YouTube lecture recording from October 2020

Complex Numbers

Imaginary numbers

Complex numbers

Complex conjugates

Modulus (size) of a complex number

Complex numbers in Python

Addition and Subtraction

Multiplication

Division

Polar Coordinates

Connection between cartesian and polar

Some examples

1

2

3

Multiplication in Polar Coordinates

A Remarkable Connection with eiθe^{i\theta}eiθ

Several important consequences

Introductory problems

Introductory problems 1

Introductory problems 2

Main problems

Main problems 1

Main problems 2

Main problems 3

Main problems 4

Main problems 5

Main problems 6

Extension problems

Extension problems 1

A Remarkable Connection with $e^{i\theta}$