Skip to main content

Scientific Computing

Essential Maths

Systems of di... []

This material has been adapted from material by Fergus Cooper from the "Essential Mathematics" module of the SABS R³ Center for Doctoral Training.

This material has been adapted from material by Fergus Cooper from the "Essential Mathematics" module of the SABS R³ Center for Doctoral Training.

Creative Commons License
This course material was developed as part of UNIVERSE-HPC, which is funded through the SPF ExCALIBUR programme under grant number EP/W035731/1

This course material was developed as part of UNIVERSE-HPC, which is funded through the SPF ExCALIBUR programme under grant number EP/W035731/1

Creative Commons License

Systems of differential equations 3

Phase Planes and Stability

YouTube lecture recording from October 2020

The following YouTube video was recorded for the 2020 iteration of the course. The material is still very similar:

Youtube lecture thumbnail

Recap from previous parts

  • 2-D linear systems can be solved analytically

  • Eigenvalues are important

  • Some larger systems can be simplified

  • Phase planes, nullclines and fixed points allow us to understand the behaviour

Example from previous lecture

x˙=x(1−x)−xy,y˙=y(2−y)−3xy.\begin{align*} \dot{x} &= x(1-x) -xy,\\ \dot{y} &= y\left(2-y\right) - 3xy. \end{align*}

Plot of the phase plane

Linear ODEs for understanding nonlinear

The decoupled ODE system

x˙=dxdt=λ1x,y˙=dydt=λ2y,\begin{align*} \dot{x} = \frac{\rm{d}x}{\rm{d}t} &= \lambda_1 x,\\ \dot{y} = \frac{\rm{d}y}{\rm{d}t} &= \lambda_2 y, \end{align*}

has a fixed point or steady state where   x˙=y˙=0  \;\dot{x}=\dot{y}=0\;, at the origin.

Solutions look like   x=Aeλ1t  \;x=Ae^{\lambda_1 t}\; and   y=Beλ2t  \;y=Be^{\lambda_2 t}\; and thus grow exponentially or shrink exponentially depending on the values of   λ1  \;\lambda_1\; and   λ2.\;\lambda_2.

If   λ1<0  \;\lambda_1 < 0\; and   λ2<0  \;\lambda_2 < 0\; then all the flow is towards the fixed point. If   λ1  \;\lambda_1\; or   λ2  \;\lambda_2\; is positive then some flow will be driven away (towards infinity).

Adding in a constant (inhomogeneous) component shifts the fixed point away from the origin. Where is the fixed point of

x˙=λ1x+10,y˙=λ2y+10?\begin{align*} \dot{x} &= \lambda_1 x + 10,\\ \dot{y} &= \lambda_2 y + 10? \end{align*}

Coupling the system has the effect of altering the principle directions over which the exponential terms apply (changing the basis).

This means that the homogeneous linear system

x˙=ax+by,y˙=cx+dy,\begin{align*} \dot{x} &= a x + b y,\\ \dot{y} &= c x + d y, \end{align*}

has a fixed point at the origin. The long-term growth or shrinkage of solutions over time is determined by the eigenvalues of the matrix

A=(abcd)\displaystyle A = \begin{pmatrix} a & b \\ c & d \end{pmatrix}

More generally, the inhomogeneous linear system

x˙=ax+by+p,y˙=cx+dy+q,\begin{align*} \dot{x} &= a x + b y + p,\\ \dot{y} &= c x + d y + q, \end{align*}

can be written

(x˙y˙)=(abcd)(xy)+(pq).\left( \begin{array}{c} \dot{x} \\ \dot{y} \end{array} \right) = \left( \begin{array}{cc} a & b \\ c& d \end{array} \right) \left( \begin{array}{c} x \\ y \end{array} \right) + \left( \begin{array}{c} p \\ q \end{array} \right) .

It has a fixed point at

(xy)=−(abcd)−1(pq).\left( \begin{array}{c} x \\ y \end{array} \right) = -\left( \begin{array}{cc} a & b \\ c& d \end{array} \right)^{-1} \left( \begin{array}{c} p \\ q \end{array} \right) .

The long-term growth or shrinkage of solutions over time is again determined by the eigenvalues of the matrix.

General nonlinear system steady states

A more general two-dimensional nonlinear system is

x˙=f(x,y),y˙=g(x,y),\begin{align*} \dot{x} &= f(x,y),\\ \dot{y} &= g(x,y), \end{align*}

where   f  \;f\; and   g  \;g\; can be any functions whatever.

We can write a polynomial (Taylor) expansion for the system when it is close to a fixed point:

  (x∗,y∗)  \displaystyle \;(x^*, y^*)\; for which   f(x∗,y∗)=g(x∗,y∗)=0.\;f(x^*,y^*)=g(x^*,y^*)=0.

x˙=f(x∗,y∗)+∂f∂x(x−x∗)+∂f∂y(y−y∗)+…,y˙=g(x∗,y∗)+∂g∂x(x−x∗)+∂g∂y(y−y∗)+…,\begin{align*} \dot{x} &= f(x^*,y^*) + \frac{\partial f}{\partial x}(x-x^*) + \frac{\partial f}{\partial y}(y-y^*) + \ldots,\\ \dot{y} &= g(x^*,y^*) + \frac{\partial g}{\partial x}(x-x^*) + \frac{\partial g}{\partial y}(y-y^*) + \ldots, \end{align*}

So, close to the fixed point:

(x˙y˙)≈(∂f∂x∂f∂y∂g∂x∂g∂y)(x−x∗y−y∗).\left( \begin{array}{c} \dot{x} \\ \dot{y} \end{array} \right) \approx \left( \begin{array}{cc} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} \\\frac{\partial g}{\partial x} & \frac{\partial g}{\partial y} \end{array} \right) \left( \begin{array}{c} x-x^* \\ y-y^* \end{array} \right) .

This means that (really close to the fixed point) we can approximate with a linear system. The eigenvalues   λ1,  λ2  \;\lambda_1,\;\lambda_2\; of the matrix

J=(∂f∂x∂f∂y∂g∂x∂g∂y)J = \left( \begin{array}{cc} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} \\\frac{\partial g}{\partial x} & \frac{\partial g}{\partial y} \end{array} \right)

will determine if a small perturbation away from   (x∗,  y∗)  \;(x^*,\;y^*)\; will decay or grow.

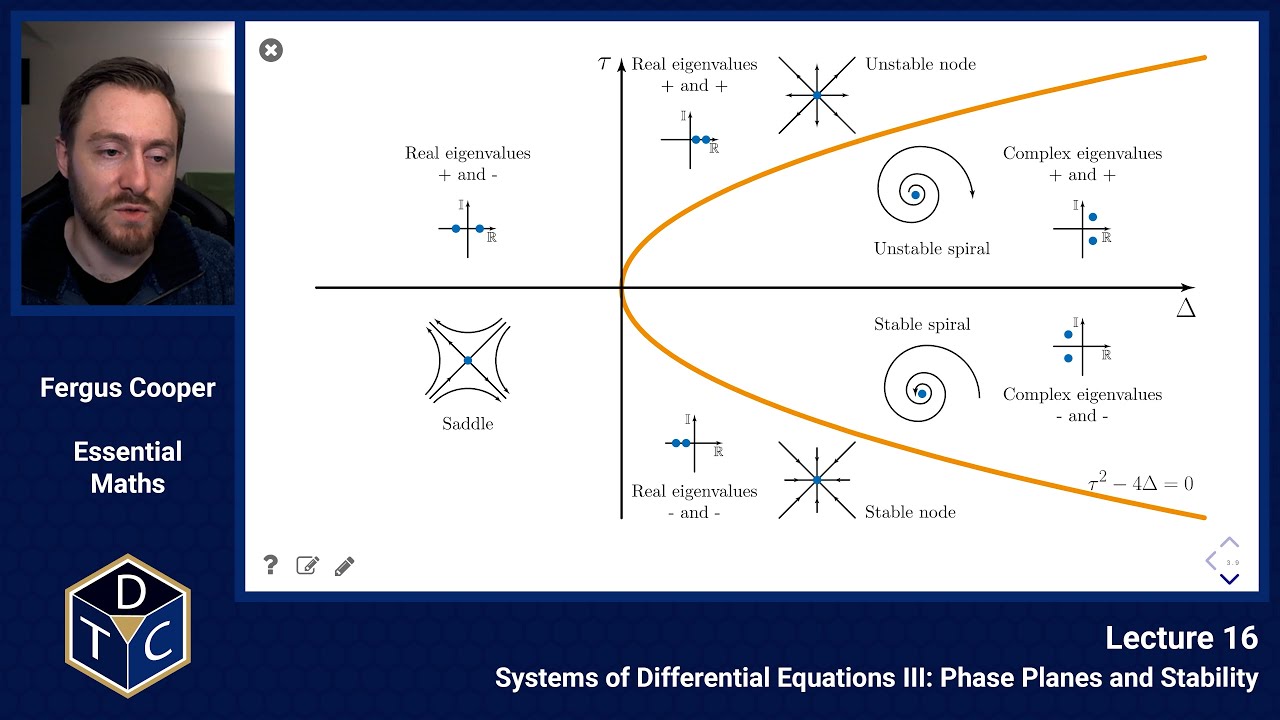
Steady state classification

J=(∂f∂x∂f∂y∂g∂x∂g∂y)J = \left( \begin{array}{cc} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} \\\frac{\partial g}{\partial x} & \frac{\partial g}{\partial y} \end{array} \right)

  • λ1<λ2<0\lambda_1<\lambda_2<0 Stable node

  • λ1=λ2<0\lambda_1=\lambda_2<0 Stable star

  • λ1>λ2>0\lambda_1>\lambda_2>0 Unstable node

  • λ1=λ2>0\lambda_1=\lambda_2>0 Unstable star

  • λ1<0<λ2\lambda_1<0<\lambda_2 Saddle (or hyperbolic) point: unstable

  • Complex λ\lambda: Spiral (with real part determining stability)

  • Imaginary λ\lambda: Neutral (solution cycles round fixed point)

The presence of negative eigenvalues determines whether a steady state is physically viable.

Eigenvalues of JJ

∣J−λI∣=∣∂f∂x−λ∂f∂y∂g∂x∂g∂y−λ∣=(∂f∂x−λ)(∂g∂y−λ)−∂f∂y∂g∂x|J-\lambda I| = \left| \begin{array}{cc} \frac{\partial f}{\partial x}-\lambda & \frac{\partial f}{\partial y} \\\frac{\partial g}{\partial x} & \frac{\partial g}{\partial y}-\lambda \end{array}\right| = \left(\frac{\partial f}{\partial x}-\lambda\right)\left(\frac{\partial g}{\partial y}-\lambda\right)-\frac{\partial f}{\partial y}\frac{\partial g}{\partial x}

So eigenvalues   λ  \;\lambda\; satisfy

λ2−λ(∂f∂x+∂g∂y)+∂f∂x∂g∂y−∂f∂y∂g∂x,\lambda^2 - \lambda\left(\frac{\partial f}{\partial x} + \frac{\partial g}{\partial y}\right) + \frac{\partial f}{\partial x}\frac{\partial g}{\partial y} - \frac{\partial f}{\partial y}\frac{\partial g}{\partial x},

or

λ2−λτ+Δwhereτ=Trace(J)andΔ=Det(J)\lambda^2 - \lambda\tau + \Delta \quad \rm{where} \quad \tau=\rm{Trace}(J) \quad and \quad \Delta = \rm{Det}(J)

Phase diagram showing different behaviour given the eigenvalues

Example system

x˙=x(1−x)−xy=f(x)y˙=y(2−y)−3xy=g(x).\begin{align*} \dot{x} &= x(1-x) -xy &=f(x)\\ \dot{y} &= y\left(2-y\right) - 3xy &=g(x). \end{align*}

  • What are the nullclines?

  • What are the fixed points?

  • What is the stability of the fixed points?

Calculate the Jacobian

J=(∂f∂x∂f∂y∂g∂x∂g∂y)=(−2x−y+1−x−3y−3x−2y+2)J = \left( \begin{array}{cc} \frac{\partial f}{\partial x} & \frac{\partial f}{\partial y} \\\frac{\partial g}{\partial x} & \frac{\partial g}{\partial y} \end{array} \right) = \left(\begin{array}{cc} -2x-y+1 & -x \\-3y & -3x-2y+2 \end{array}\right)

At (0,0)(0,0):

J(0,0)=(1002)J_{(0,0)} = \left(\begin{array}{cc} 1 & 0 \\0 & 2 \end{array}\right)
∣1−λ002−λ∣  ⟹  λ1=1,  λ2=2(unstable)\left|\begin{array}{cc} 1-\lambda & 0 \\0 & 2-\lambda\end{array}\right|\quad\implies\quad\lambda_1 = 1, \; \lambda_2 = 2 \qquad\rm{(unstable)}

At (1/2,1/2)(1/2,1/2):

J(1/2,1/2)=(−12−12−32−12)J_{(1/2,1/2)} = \left(\begin{array}{cc} -\frac{1}{2} & -\frac{1}{2} \\-\frac{3}{2} & -\frac{1}{2} \end{array}\right)
∣−12−λ−12−32−12−λ∣  ⟹  λ±=12±32(saddle)\left|\begin{array}{cc} -\frac{1}{2}-\lambda & -\frac{1}{2} \\-\frac{3}{2} & -\frac{1}{2}-\lambda\end{array}\right|\quad\implies\quad\lambda_\pm = \frac{1}{2} \pm \frac{\sqrt{3}}{2} \qquad\rm{(saddle)}

At (1,0)(1,0):

J(1,0)=(−1−10−1)J_{(1,0)} = \left(\begin{array}{cc} -1 & -1 \\ 0 & -1 \end{array}\right)
∣−1−λ−10−1−λ∣  ⟹  λ1=λ2=−1(stable)\left|\begin{array}{cc} -1-\lambda & -1 \\0 & -1-\lambda\end{array}\right|\quad\implies\quad\lambda_1 = \lambda_2 = -1 \qquad\rm{(stable)}

At (0,2)(0,2):

J(0,2)=(−10−6−2)J_{(0,2)} = \left(\begin{array}{cc} -1 & 0 \\ -6 & -2 \end{array}\right)
∣−1−λ0−6−2−λ∣  ⟹  λ1=−1,  λ2=−2(stable)\left|\begin{array}{cc} -1-\lambda & 0 \\-6 & -2-\lambda\end{array}\right|\quad\implies\quad\lambda_1 = -1, \; \lambda_2 = -2 \qquad\rm{(stable)}

If we now look again at the phase plane, after having calculated the stability of the fixed points, we can see that the arrows move towards the stable fixed points, and away from the unstable ones.

Plot of the phase plane

Summary

  • Eigenvalues tell us about the behaviour of linear systems

  • Eigenvalues tell us about the stability of nonlinear systems

Main problems

These questions are extensions of questions on the previous page.

Main problems 1

Classify the fixed points and discuss stability of the following linear systems:

  1. x˙=x+3y,y˙=−6x+5y;\displaystyle \dot{x} = x+3y, \qquad \dot{y}=-6x+5y;

  2. x˙=x+3y+4,y˙=−6x+5y−1;\displaystyle \dot{x} = x+3y+4, \qquad \dot{y}=-6x+5y-1;

  3. x˙=x+3y+1,y˙=−6x+5y.\displaystyle \dot{x} = x+3y+1, \qquad \dot{y}=-6x+5y.

Main problems 2

Classify the fixed points and discuss stability of the following nonlinear systems:

  1. x˙=−4y+2xy−8y˙=4y2−x2;\displaystyle \dot{x} = -4y+2xy-8 \qquad \dot{y}=4y^2-x^2;

  2. x˙=y−x2+2,y˙=2(x2−y2).\displaystyle \dot{x} = y-x^2+2, \qquad \dot{y}=2(x^2-y^2).

Main problems 3

The population of a host, H(t)H(t), and a parasite, P(t)P(t), are described approximately by the equations

dHdT=(a−bP)H,dPdT=(c−dPH)P,H>0,\displaystyle \def\dd#1#2{{\frac{{\rm d}#1}{{\rm d}#2}}} \dd{H}{T}=(a-bP)H,\qquad \dd{P}{T}=(c-\frac{dP}{H})P, \qquad H>0,

where a,b,c,da,b,c,d are positive constants. Previously, by a change of scales, these equations were put in the simpler form

y˙=(1−x)y,x˙=αx(1−xy),\displaystyle \def\dd#1#2{{\frac{{\rm d}#1}{{\rm d}#2}}} \dot{y} = (1-x)y, \qquad \dot{x}=\alpha x(1-\frac{x}{y}),

where α=ca\displaystyle \alpha=\frac{c}{a}.

Find and classify the fixed points of these simplified equations. Sketch the phase flow diagram including these fixed points and the information from the previous sketch. That is, include the flow across:

  1. y=x\displaystyle y=x;

  2. x=0\displaystyle x=0;

  3. y=0\displaystyle y=0;

  4. x=1\displaystyle x=1;

  5. y=βx\displaystyle y=\beta x, for β\beta greater than and less than 1.

Main problems 4

In the previous parts of this question a model of fish and anglers was developed and simplified. This question analyses the simplified model.

The simplified version of the model is

x˙=rx(1−x)−xy,y˙=βx−y\displaystyle \dot{x} = rx(1 - x) - xy,\qquad \dot{y} = \beta x - y

where xx and yy represent fish and angler populations, respectively. The x˙\dot{x} notation represents the derivative with respect to non-dimensional time.

  1. Calculate the steady states of the system.

  2. Determine the stability of the fixed points in the case β=r=4\beta = r = 4.

  3. Draw the phase plane, including the nullclines and phase trajectories.

Extension problems

Extension problems 1

A population FF of foxes feeds on a population HH of hares. A model for the changes in the population is given by

dHdT=aH−bHF(H>0),dFdT=cHF−dF(F>0).\def\dd#1#2{{\frac{{\rm d}#1}{{\rm d}#2}}} \begin{aligned} \dd{H}{T} &= aH-bHF\quad &(H>0),\\ \dd{F}{T} &= cHF-dF\quad &(F>0). \end{aligned}

  1. Define the four variables a,b,c,da,b,c,d.

  2. Find the fixed point of the system and describe the motion in its neighbourhood.

  3. What does this mean in terms of the population of hares and foxes?