Differential equations 3
Steady State Solutions and Mass Action
YouTube lecture recording from October 2020
The following YouTube video was recorded for the 2020 iteration of the course. The material is still very similar:
Steady-state solutions
It is often useful to find the steady state of a system described by ordinary differential equations
This occurs when all rates (i.e. derivatives) are zero
A steady state may be stable or unstable, depending on whether or not small deviations from the steady state tend to be corrected or amplified
We can evaluate the stability of a steady state by considering the sign of the derivative nearby
Example 1: radioactive decay
Recall the radioactive decay equation
Let us examine a plot of the solution, , and the gradient as functions of time:
Here the steady state occurs when , and is 'reached' after infinite time.
For small positive the derivative is negative, moving the system towards the steady state.
Physical considerations show that negative is impossible, hence the steady state is stable as we would expect.
Example 2: production and degradation of a protein
Consider a simple model of the production and degradation of a protein, shown by the reaction chain where and are reaction rates, and let .
We can represent the change in concentration of the protein by
so the steady state occurs when .
Mass action
Consider, again, the reaction chain:
Suppose the reaction is governed by "mass action" kinetics, so (constant) and .
The equation is then
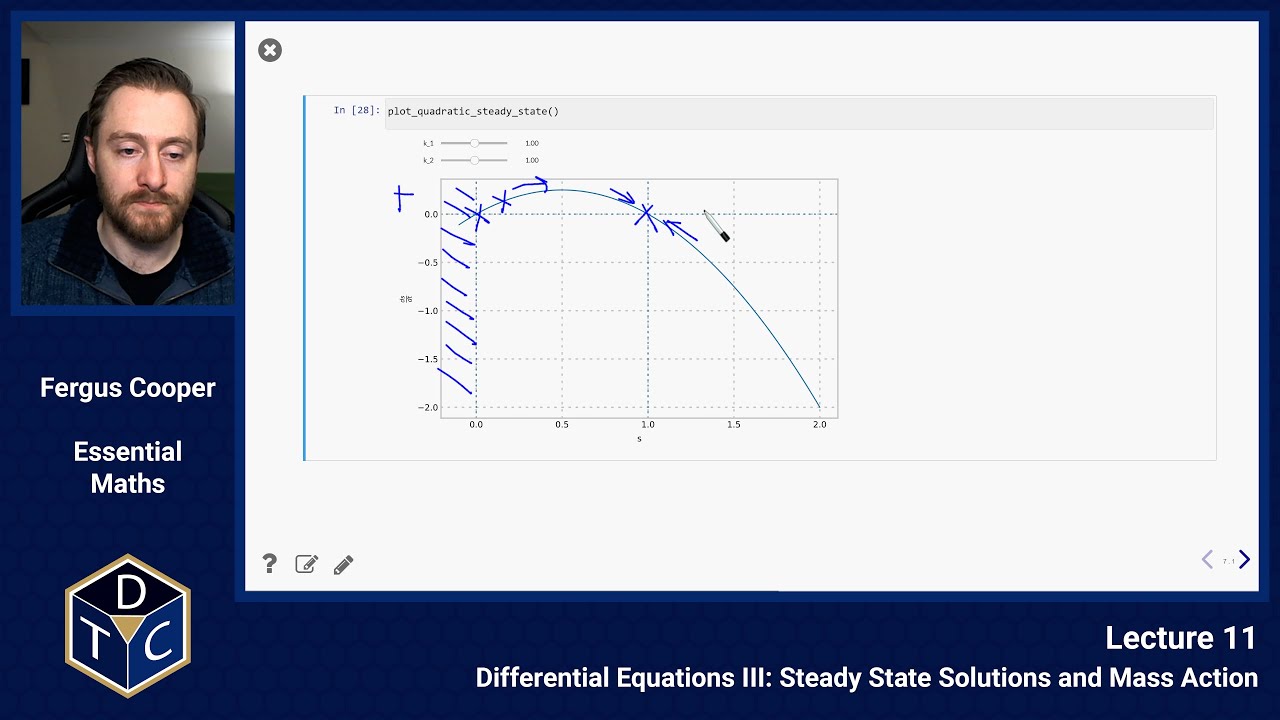
The steady state is given by , and it is stable:
We can see that it is stable by examining the graph:
If we move to the left of , the gradient is positive, so we move back towards
If we move to the right of , the gradient is negative, so we, again, move back towards
We can solve the differential equation by separation of variables.
Thus, the concentration of relaxes exponentially to the steady state, no matter the initial condition.
If the initial concentration of is given by then
To understand different possibilities for these steady states, let us suppose instead that enhances its own production (positive feedback) and the degradation rate is nonlinear.
If we were to have the following form for and :
then:
This system will be at steady state when , i.e.
or
We can plot versus to see if they are stable or unstable. Here, :
The local behaviour near the fixed point as is the same as in the previous plot, so we can immediately see that it is a stable steady state
The local behaviour near the fixed point at is the opposite: moving one way or the other, the gradient will take even further away
Non-graphical method
Let us investigate this same behaviour in a more rigorous manner.
When is small (and positive, since it is a concentration) so the derivative will be positive, making an unstable steady state.
For the other steady state, consider small deviations by from the steady state, e.g. .
Then:
The derivative (after substituting and into the original differential equation) is:
.
It is, since , negative, pushing back towards the steady state, hence it is a stable steady state.
Example: the logistic equation
The growth of a cell colony can be modelled by the logistic equation
where is the number of cells at time and and are constant parameters (both positive).
The steady state for the system, or equilibrium population size, occurs when the growth rate is zero, i.e.
Here is a plot, for :
for small positive , and so and the population size will increase, meaning that is an unstable steady state.
In fact the growth rate is positive for and negative for , making a stable steady state.
We can solve the differential equation to examine the transient behaviour. This is a separable equation, so
This can be solved using partial fractions on the left hand side:
With initial conditions you get
Summary of first order differential equations
To solve a differential equation:
Calculate the general solution
Try to write it as a separable equation first
Other methods (e.g. integrating factors) not covered in this course
This general solution will include an arbitrary constant this may be eliminated using initial conditions (if these are given)
Can check your solution numerically using Python
To find steady state (equilibrium) solutions, find points where all (first) derivatives are zero.
To determine stability of these steady states, look at the behaviour of the first derivative in the vicinity of the steady state. You can sketch the first derivative, or use Python to help with this.
Chemical reactions to equations: mass action
Under the law of mass action, we assume the following:
that chemical reactions have uniform mixing
that rates are proportional to the product of the masses of the reactants
that predator/prey interactions, and epidemics, have similar rules
Let us look at some examples:
A and B produce C. The reaction is governed by A meeting B:
Then we get the following differential equations:
> >
Predation of R by W
Gives the following differential equation:
Constant production (zeroth order)
Gives the following differential equation:
Degradation/death
Gives the following differential equation:
Numerically solving differential equations
What if we can't solve the differential equation (or don't want to)?
Euler's method
Given a differential equation
with initial state we can approximate the state at as:
and the next state as
and so on!
This mean's we can estimate the entire time course of , provided:
We can calculate (or approximate it with a computer)
We're patient enough to take really tiny steps
We have already seen examples of this, using SciPy's ODEInt function, although this uses more sophisticated methods than the one described here.
Introductory problems
Introductory problems 1
Determine the steady states are their stabilities, for each of the following:
, where is a positive constant
, where and are constants
, where and are negative constants
Main problems
Main problems 1
Not all chemical systems relax exponentially to steady state. Consider the bimolecular decay reaction
Assuming is a mass action constant, form and solve a differential equation representing the change in concentration of .
If you should get
Main problems 2
The model is an appropriate model for diseases that mutate quickly and can therefore infect people multiple times, such as the common cold or sexually transmitted infections like gonorrhea and chlamydia.
In the model, individuals are 'susceptible' until they are 'infected', and then they return to being 'susceptible' again. Infection requires the interaction of susceptible individuals with infected individuals and therefore follows the law of mass action, whereas the rate at which an individual becomes susceptible again after infection is constant.
Let and be the proportions of the population that are susceptible and infected. If infection happens at rate and recovery happens at rate , write down differential equations for and .
Noting that and are proportions of the population, which is assumed constant, reduce the system to a single differential equation in terms of . In other words, write down a single equation, involving just and its derivative.
Find both steady states of . Under what conditions on and are each attainable?
Without solving the differential equation, sketch the behaviour of and over time, starting with a small quantity of infected individuals. Illustrate how both steady states may be achieved.
Main problems 3
Consider a closed reaction system consisting of a single reversible reaction:
where and are mass action coefficients.
Formulate a pair of coupled differential equations for the change in concentration of and .
Noting that the total concentration of reactants is constant (), reduce the system of equations to a single differential equation. In other words, write down a single equation, involving either just and its derivative, or just and its derivative.
Find the steady-state concentrations of and .
Solve the single differential equation to reveal the transient behaviour. Sketch the behaviour for different illustrative initial conditions.
Main problems 4
Consider the simple model
in which species is produced at a fixed rate and consumed via Michaelis-Menten kinetics. Find the steady state of , and verify that it is stable for any non-negative parameter values, provided .
Main problems 5
Recall the simple model of the production and degradation of a protein from the lecture, shown by the reaction chain
where and are reaction rates rather than mass action coefficients.
Suppose and . Write down a differential equation describing the rate of change of S, and find the steady state concentration of S in terms of the two parameters and (i.e. the concentration at which the rate of change is zero). At what rate is S being produced in steady state?
Now suppose that
and take the parameter values to be . Determine the number of steady states and the type of each.
Extension problems
Extension problems 1
Various mathematical models have been proposed for the initial growth of solid tumours, and some are summarised in The Model Muddle: In Search of Tumor Growth Laws. They are differential equations describing the rate of change of tumour volume as a function of time , for example:
Solve each equation both analytically and numerically, using Python. As was done in Figure 1A in the paper, compare the behaviours of the different growth laws over a suitable time interval for an initially small tumour, again using Python.
Extension problems 2
Find the solution to the following differential equations subject to the specified boundary conditions, using integrating factors:
Extension problems 3
Consider the second order differential equation
Show that is a solution to this equation for some complex numbers , and real constants , .
Recalling that any complex number can be written as , what does this tell you about the nature of the solution?
If and what is the particular solution of the differential equation?