Analyzing and Visualizing Data
For this lesson, you will first need to download and unzip uniqplus_python_data.zip.
Words are useful, but what's more useful are the sentences and stories we build with them. Similarly, while a lot of powerful, general tools are built into Python, specialized tools built up from these basic units live in libraries that can be called upon when needed.
Loading data into Python
To begin processing inflammation data, we need to load it into Python. One way we can accomplish this is using a library called NumPy, which stands for Numerical Python. In general, you should be using this library whenever you want to do fancy things with lots of numbers, especially if you have matrices or arrays. To tell Python that we'd like to start using NumPy, we need to import it:
import numpy
Importing a library is like getting a piece of lab equipment out of a storage locker and setting it up on the bench. Libraries provide additional functionality to the basic Python package, much like a new piece of equipment adds functionality to a lab space. Just like in the lab, importing too many libraries can sometimes complicate and slow down your programs - so we only import what we need for each program.
Once we've imported the library, we can ask the library to read our data file for us:
numpy.loadtxt(fname='inflammation-01.csv', delimiter=',')
numpy.array([[ 0., 0., 1., ..., 3., 0., 0.], [ 0., 1., 2., ..., 1., 0., 1.], [ 0., 1., 1., ..., 2., 1., 1.], ..., [ 0., 1., 1., ..., 1., 1., 1.], [ 0., 0., 0., ..., 0., 2., 0.], [ 0., 0., 1., ..., 1., 1., 0.]])
The expression numpy.loadtxt(...) is a function call that asks Python to run the function loadtxt which belongs to the numpy library.
This dotted notation is used everywhere in Python: the thing that appears before the dot contains the thing that appears after.
As an example, John Smith is the John that belongs to the Smith family.
We could use the dot notation to write his name smith.john,
just as loadtxt is a function that belongs to the numpy library.
numpy.loadtxt has two parameters: the name of the file we want to read and the delimiter that separates values on a line.
These both need to be character strings (or strings for short), so we put them in quotes.
Since we haven't told it to do anything else with the function's output, the notebook displays it.
This happens whenever we call a function withou an associated variable assignemnt, that functions outputs are displayed instead.
In this case, that output is the data we just loaded.
By default, only a few rows and columns are shown (with ... to omit elements when displaying big arrays).
Note that, to save space when displaying NumPy arrays, Python does not show us trailing zeros, so 1.0 becomes 1..
Our call to numpy.loadtxt read our file but didn't save the data in memory so we have no way of now accessing it.
To do that, we need to assign the array to a variable when calling the function.
In a similar manner to how we assign a single value to a variable,
we can also assign an array of values to a variable using the same syntax.
Let's re-run numpy.loadtxt and save the returned data:
data = numpy.loadtxt(fname='inflammation-01.csv', delimiter=',')
This statement doesn't produce any output because we've assigned the output to the variable data.
If we want to check that the data have been loaded,
we can print the variable's value:
print(data)
[[ 0. 0. 1. ..., 3. 0. 0.] [ 0. 1. 2. ..., 1. 0. 1.] [ 0. 1. 1. ..., 2. 1. 1.] ..., [ 0. 1. 1. ..., 1. 1. 1.] [ 0. 0. 0. ..., 0. 2. 0.] [ 0. 0. 1. ..., 1. 1. 0.]]
Now that the data are in memory, we can manipulate them.
First, let's ask what type of thing data refers to:
print(type(data))
<class 'numpy.ndarray'>
The output tells us that data currently refers to
an N-dimensional array, the functionality for which is provided by the NumPy library.
These data correspond to arthritis patients' inflammation.
The rows are the individual patients, and the columns
are their daily inflammation measurements.
Data Type
A Numpy array contains one or more elements of the same type.
The type function will only tell you that a variable is a NumPy array but won't tell you the type of thing inside the array.
We can find out the type of the data contained in the NumPy array.
print(data.dtype)
float64
Likewise, we can use type to find out the type of a single value, this can be useful when dealing with other data structures.
type(data[0,0])
This tells us that the NumPy array's elements are floating point numbers.
With the following command, we can see the array's shape:
print(data.shape)
(60, 40)
The output tells us that the data array variable contains 60 rows and 40 columns. When we
created the variable data to store our arthritis data, we did not only create the array; we also
created information about the array, called members or
attributes. This extra information describes data in the same way an adjective describes a noun.
data.shape is an attribute of data which describes the dimensions of data. We use the same
dotted notation for the attributes of variables that we use for the functions in libraries because
they have the same part-and-whole relationship.
If we want to get a single number from the array, we must provide an index in square brackets after the variable name, just as we do in math when referring to an element of a matrix. Our inflammation data has two dimensions, so we will need to use two indices to refer to one specific value:
print('first value in data:', data[0, 0])
first value in data: 0.0
print('middle value in data:', data[30, 20])
middle value in data: 13.0
The expression data[30, 20] accesses the element at row 30, column 20. While this expression may
not surprise you, data[0, 0] might.
Some programming languages like Fortran, MATLAB and R start counting at 1
because that's what human beings have done for thousands of years.
Languages in the C family (including C++, Java, Perl, and Python) count from 0
because it represents an offset from the first value in the array (the second
value is offset by one index from the first value).
This is closer to the way that computers represent arrays (if you are interested in the historical
reasons behind counting indices from zero, you can read
Mike Hoye's blog post).
As a result, if we have an M×N array in Python, its indices go from 0 to M-1 on the first axis and 0 to N-1 on the second.
It takes a bit of getting used to, but one way to remember the rule is that the index is how many steps we have to take from the start to get the item we want.
Corner indices
What may also surprise you is that when Python displays an array,
it shows the element with index [0, 0] in the upper left corner rather than the lower left.
This is consistent with the way mathematicians draw matrices but different from the Cartesian coordinates.
The indices are (row, column) instead of (column, row) for the same reason,
which can be confusing when plotting data.
Slicing data
An index like [30, 20] selects a single element of an array, but we can select whole sections as well.
For example, we can select the first ten days (columns) of values
for the first four patients (rows) like this:
print(data[0:4, 0:10])
[[ 0. 0. 1. 3. 1. 2. 4. 7. 8. 3.] [ 0. 1. 2. 1. 2. 1. 3. 2. 2. 6.] [ 0. 1. 1. 3. 3. 2. 6. 2. 5. 9.] [ 0. 0. 2. 0. 4. 2. 2. 1. 6. 7.]]
The slice 0:4 means, "Start at index 0 and go up to, but not including, index 4".
Similar to "arrays start at 0", the up-to-but-not-including takes a bit of getting used to,
but the rule is that the difference between the upper and lower bounds is the number of values in the slice.
We can start slices at any index we need,
print(data[5:10, 0:10])
[[ 0. 0. 1. 2. 2. 4. 2. 1. 6. 4.] [ 0. 0. 2. 2. 4. 2. 2. 5. 5. 8.] [ 0. 0. 1. 2. 3. 1. 2. 3. 5. 3.] [ 0. 0. 0. 3. 1. 5. 6. 5. 5. 8.] [ 0. 1. 1. 2. 1. 3. 5. 3. 5. 8.]]
We also don't have to include the upper and lower bound on the slice. If we don't include the lower bound, Python uses 0 by default; if we don't include the upper, the slice runs to the end of the axis, and if we don't include either (i.e., if we use ':' on its own), the slice includes everything:
small = data[:3, 36:] print('small is:') print(small)
The above example selects rows 0 through 2 and columns 36 through to the end of the array.
small is: [[ 2. 3. 0. 0.] [ 1. 1. 0. 1.] [ 2. 2. 1. 1.]]
Selecting every nth item
We can also select only every nth element in an array by using double colons in our slices,
print(data[::3, ::2])
selects every 3rd row and every 2nd column.
We can also combine this with a start and stop index, with the form [start:stop:step],
print(data[0:10:3, 0:10:2])
will again select every 3rd row and every 2nd column, but only up to the 10th row and 10th column.
Analyzing data
NumPy has several useful functions that take an array as input to perform operations on its values.
If we want to find the average inflammation for all patients on all days, for example, we can ask NumPy to compute data's mean value:
print(numpy.mean(data))
6.14875
mean is a function that takes an array as an argument.
Not All Functions Have Input
Generally, a function uses inputs to produce outputs. However, some functions produce outputs without needing any input. For example, checking the current time doesn't require any input.
import time print(time.ctime())
Sat Mar 26 13:07:33 2016
For functions that don't take in any arguments, we still need parentheses (()) to tell Python to go and do something for us.
Let's use three other NumPy functions to get some informative values about the dataset. We'll also use multiple assignment, a convenient Python feature that will enable us to do this all in one line.
maxval, minval, stdval = numpy.max(data), numpy.min(data), numpy.std(data) print('maximum inflammation:', maxval) print('minimum inflammation:', minval) print('standard deviation:', stdval)
Here we've assigned the return value from numpy.max(data) to the variable maxval, the value
from numpy.min(data) to minval, and so on.
maximum inflammation: 20.0 minimum inflammation: 0.0 standard deviation: 4.61383319712
Mystery Functions in IPython
How did we know what functions NumPy has and how to use them?
If you are working in IPython or in a Jupyter Notebook, there is an easy way to find out.
If you type the name of something followed by a dot, then you can use tab completion
(e.g. type numpy. and then press Tab)
to see a list of all functions and attributes that you can use.
After selecting one, you can also add a question mark (e.g. numpy.cumprod?),
and IPython will return an explanation of the method!
This is the same as doing help(numpy.cumprod).
Similarly, if you are using the "plain vanilla" Python interpreter, you can type numpy.
and press the Tab twice for a listing of what is available. You can then use the
help() function to see an explanation of the function you're interested in,
for example: help(numpy.cumprod).
When analyzing data, though, we often want to look at variations in statistical values, such as the maximum inflammation per patient or the average inflammation per day. One way to do this is to create a new temporary array of the data we want, then ask it to do the calculation:
patient_0 = data[0, :] # 0 on the first axis (rows), everything on the second (columns) print('maximum inflammation for patient 0:', numpy.max(patient_0))
maximum inflammation for patient 0: 18.0
Everything in a line of Python code following the '#' symbol is a comment that is ignored by Python. Comments allow programmers to leave explanatory notes for other programmers or their future selves.
We don't actually need to store the row in a variable of its own. Instead, we can combine the selection and the function call:
print('maximum inflammation for patient 2:', numpy.max(data[2, :]))
maximum inflammation for patient 2: 19.0
What if we need the maximum inflammation for each patient over all days (as in the next diagram on the left) or the average for each day (as in the diagram on the right)? As the diagram below shows, we want to perform the operation across an axis:
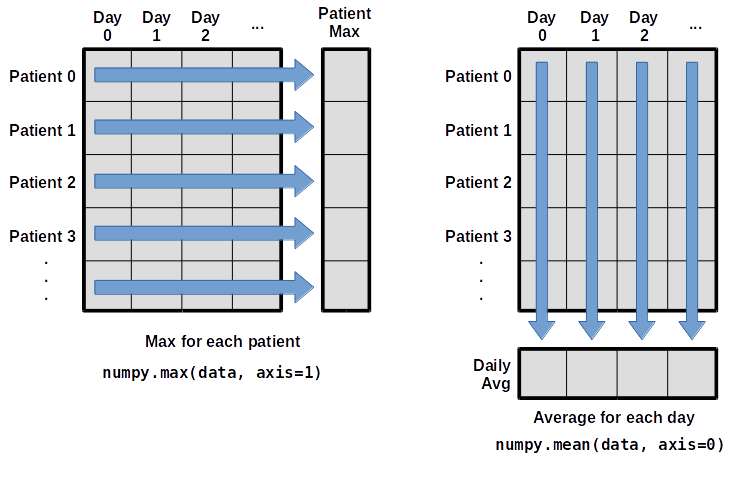
To support this functionality, most array functions allow us to specify the axis we want to work on. If we ask for the average across axis 0 (rows in our 2D example), we get:
print(numpy.mean(data, axis=0))
[ 0. 0.45 1.11666667 1.75 2.43333333 3.15 3.8 3.88333333 5.23333333 5.51666667 5.95 5.9 8.35 7.73333333 8.36666667 9.5 9.58333333 10.63333333 11.56666667 12.35 13.25 11.96666667 11.03333333 10.16666667 10. 8.66666667 9.15 7.25 7.33333333 6.58333333 6.06666667 5.95 5.11666667 3.6 3.3 3.56666667 2.48333333 1.5 1.13333333 0.56666667]
As a quick check, we can ask this array what its shape is:
print(numpy.mean(data, axis=0).shape)
(40,)
The expression (40,) tells us we have an N×1 vector, so this is the average inflammation per day for all patients.
If we average across axis 1 (columns in our 2D example), we get:
print(numpy.mean(data, axis=1))
[ 5.45 5.425 6.1 5.9 5.55 6.225 5.975 6.65 6.625 6.525 6.775 5.8 6.225 5.75 5.225 6.3 6.55 5.7 5.85 6.55 5.775 5.825 6.175 6.1 5.8 6.425 6.05 6.025 6.175 6.55 6.175 6.35 6.725 6.125 7.075 5.725 5.925 6.15 6.075 5.75 5.975 5.725 6.3 5.9 6.75 5.925 7.225 6.15 5.95 6.275 5.7 6.1 6.825 5.975 6.725 5.7 6.25 6.4 7.05 5.9 ]
which is the average inflammation per patient across all days.
Slicing Strings
A section of an array is called a slice. We can take slices of character strings as well:
element = 'oxygen' print('first three characters:', element[0:3]) print('last three characters:', element[3:6])
first three characters: oxy last three characters: gen
What is the value of element[:4]?
What about element[4:]?
Or element[:]?
What is element[-1]?
What is element[-2]?
Given those answers, explain what element[1:-1] does.
How can we rewrite the slice for getting the last three characters of element, so that it works even if we assign a different string to element?
Test your solution with the following strings: carpentry, clone, hi.
Thin Slices
The expression element[3:3] produces an empty string i.e., a string that contains no characters.
If data holds our array of patient data, what does data[3:3, 4:4] produce? What about data[3:3, :]?
Stacking Arrays
Arrays can be concatenated and stacked on top of one another.
We can use NumPy's vstack and hstack functions for vertical and horizontal stacking respectively.
import numpy A = numpy.array([[1,2,3], [4,5,6], [7, 8, 9]]) print('A = ') print(A) B = numpy.hstack([A, A]) print('B = ') print(B) C = numpy.vstack([A, A]) print('C = ') print(C)
A = [[1 2 3] [4 5 6] [7 8 9]] B = [[1 2 3 1 2 3] [4 5 6 4 5 6] [7 8 9 7 8 9]] C = [[1 2 3] [4 5 6] [7 8 9] [1 2 3] [4 5 6] [7 8 9]]
Write some additional code that slices the first and last columns of A, and stacks them into a 3x2 array.
Make sure to print the results to verify your solution.
Change In Inflammation
The patient data is longitudinal in the sense that each row represents a series of observations relating to one individual. This means that the change in inflammation over time is a meaningful concept. Let's find out how to calculate changes in the data contained in an array with NumPy.
The numpy.diff() function takes an array and returns the differences between two successive values.
Let's use it to examine the changes each day across the first week of patient 3 from our inflammation dataset.
patient3_week1 = data[3, :7] print(patient3_week1)
[0. 0. 2. 0. 4. 2. 2.]
Calling numpy.diff(patient3_week1) would do the following calculations:
[ 0 - 0, 2 - 0, 0 - 2, 4 - 0, 2 - 4, 2 - 2 ]
and return the 6 difference values in a new array.
numpy.diff(patient3_week1)
numpy.array([ 0., 2., -2., 4., -2., 0.])
Note that the array of differences is shorter by one element (length 6).
When calling numpy.diff with a multi-dimensional array, an axis argument may be passed to the function to specify which axis to process.
When applying numpy.diff to our 2D inflammation array data, which axis would we specify?
If the shape of an individual data file is (60, 40) (60 rows and 40 columns),
what would the shape of the array be after you run the diff() function and why?
How would you find the largest change in inflammation for each patient? Does it matter if the change in inflammation is an increase or a decrease?
Visualizing data
The mathematician Richard Hamming once said, "The purpose of computing is insight, not numbers," and the best way to develop insight is often to visualize data.
Visualization deserves an entire lecture of its own, but we can explore a few features of Python's matplotlib library here.
While there is no official plotting library, matplotlib is the de facto standard.
First, we will import the pyplot module from matplotlib and use two of its functions to create and display a heat map of our data:
import matplotlib.pyplot image = matplotlib.pyplot.imshow(data) matplotlib.pyplot.show()
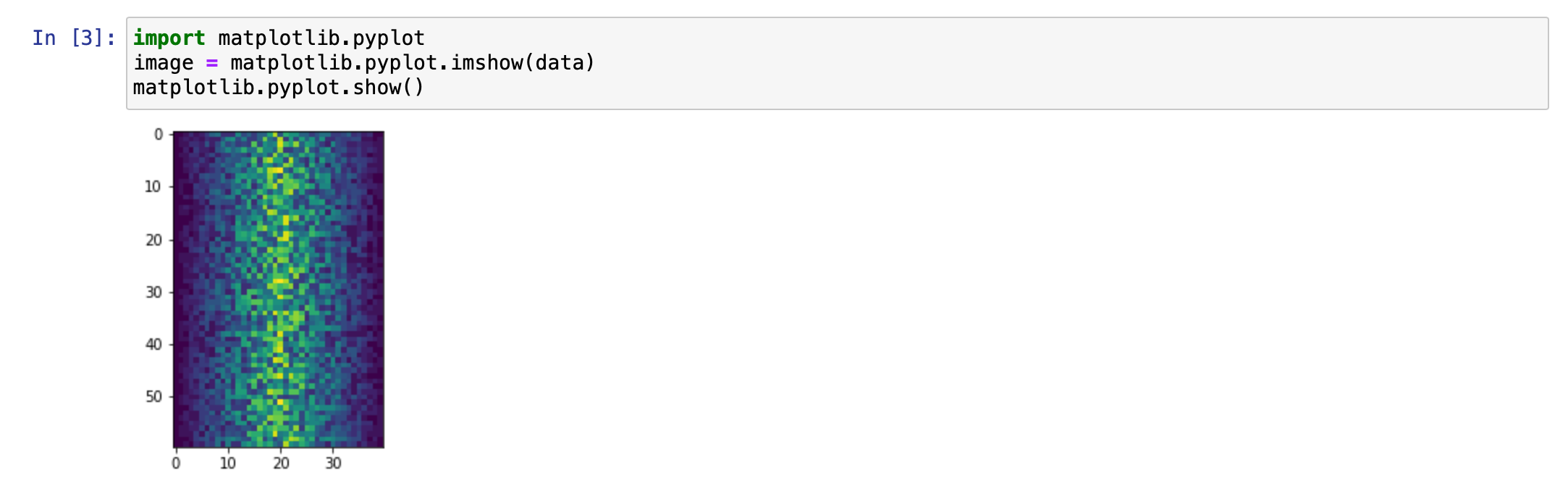
Blue pixels in this heat map represent low values, while yellow pixels represent high values. As we can see, inflammation rises and falls over a 40-day period. Let's take a look at the average inflammation over time:
ave_inflammation = numpy.mean(data, axis=0) ave_plot = matplotlib.pyplot.plot(ave_inflammation) matplotlib.pyplot.show()
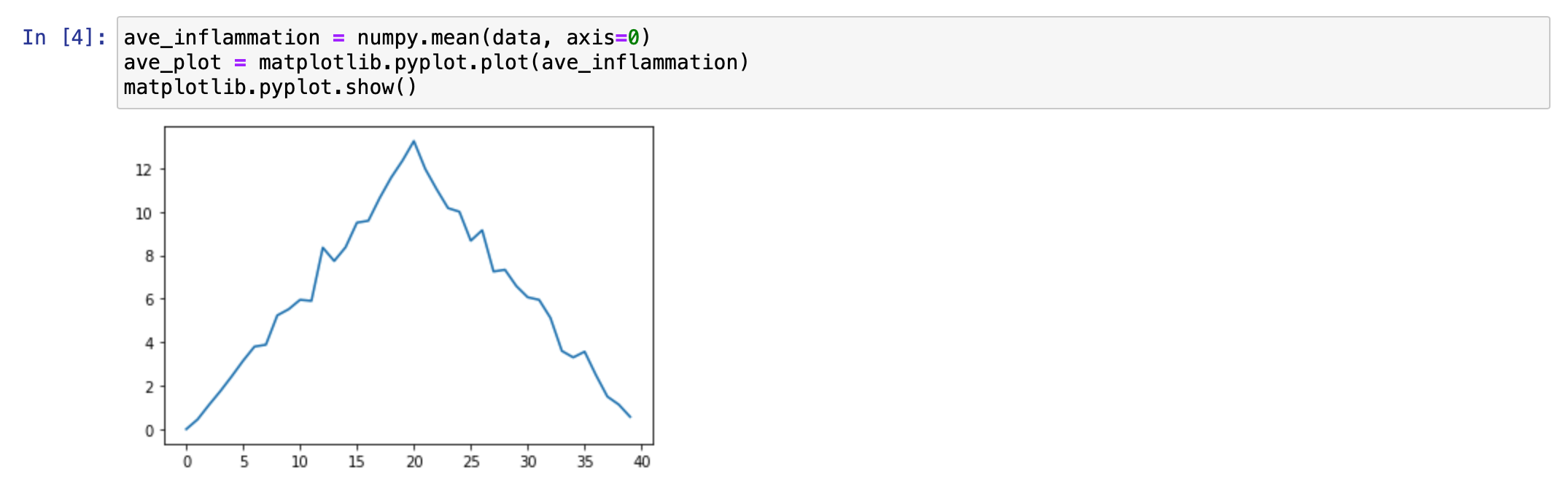
Here, we have put the average inflammation per day across all patients in the variable ave_inflammation,
then asked matplotlib.pyplot to create and display a line graph of those values.
The result is a roughly linear rise and fall, which is suspicious:
we might instead expect a sharper rise and slower fall.
Let's have a look at two other statistics:
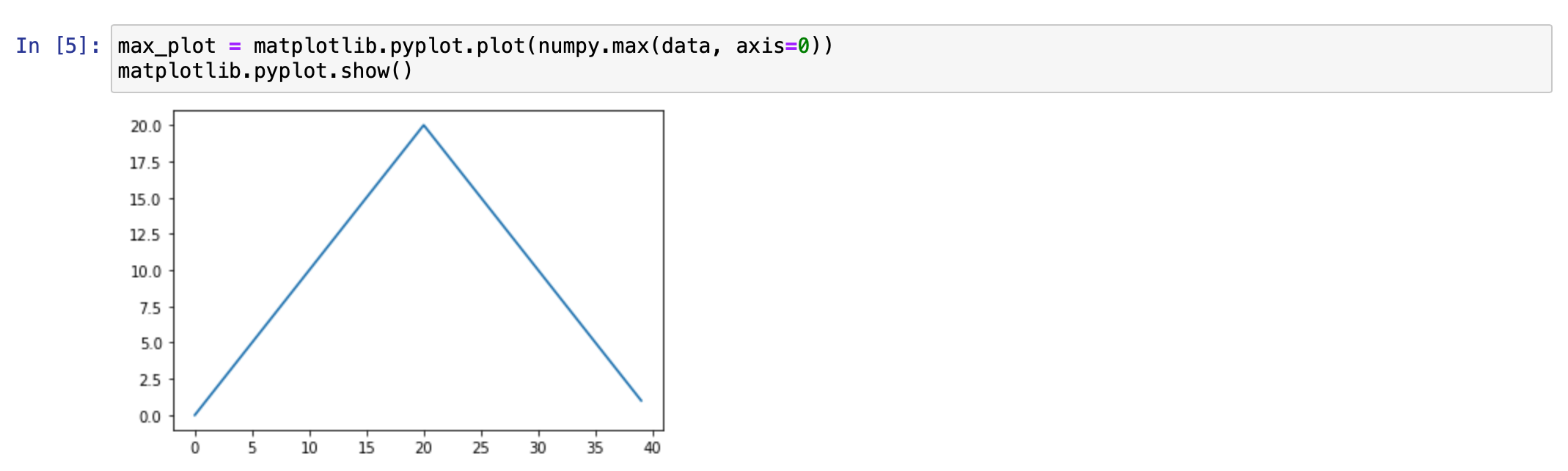
max_plot = matplotlib.pyplot.plot(numpy.max(data, axis=0)) matplotlib.pyplot.show()
min_plot = matplotlib.pyplot.plot(numpy.min(data, axis=0)) matplotlib.pyplot.show()
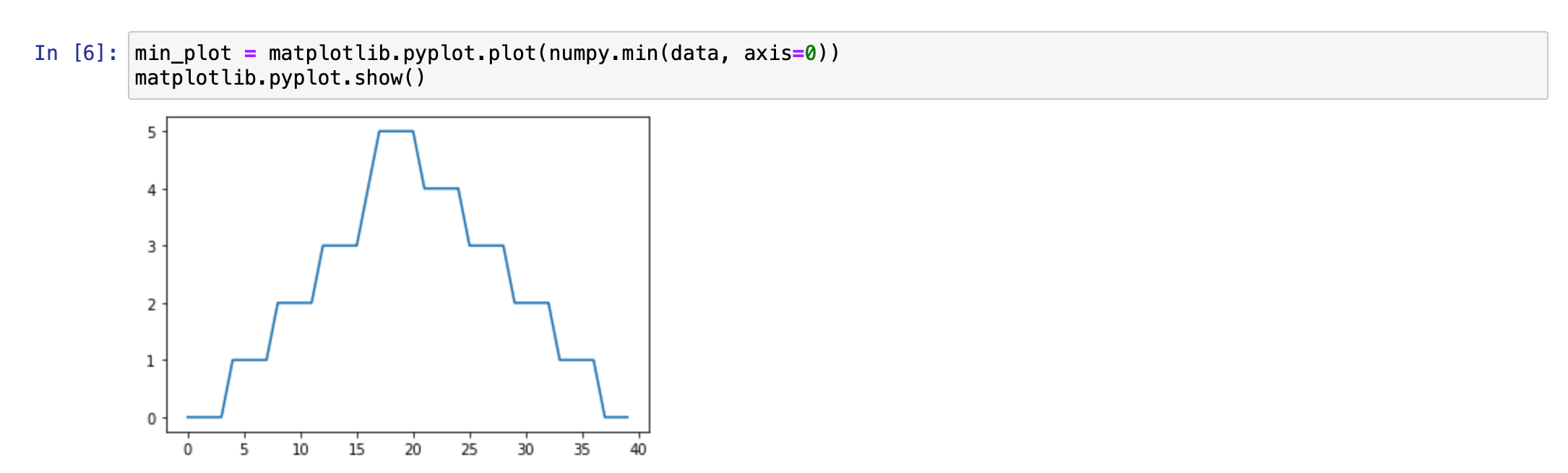
The maximum value rises and falls smoothly, while the minimum seems to be a step function. Neither trend seems particularly likely, so either there's a mistake in our calculations or something is wrong with our data. This insight would have been difficult to reach by examining the numbers themselves without visualization tools.
Multiple figure plots
You can group similar plots in a single figure using subplots. This script below uses a number of new commands.
The function
matplotlib.pyplot.figure()creates a space into which we will place all of our plots.This function returns a
Figureobject.This is sometimes refered to as a "handle" to the figure, which can be used to change the figure's properties.
The parameter
figsizetells Python how big to make this space.Each subplot is placed into the figure using its
add_subplotmethod.Like "figure", this method returns an
Axesobject, allowing us to interact with axes.
The
add_subplotmethod takes 3 parameters.The first denotes how many total rows of subplots there are
The second parameter refers to the total number of subplot columns,
The final parameter denotes which subplot your variable is referencing (left-to-right, top-to-bottom).
The "handle" for each subplot is stored in a different variable (
axes1,axes2,axes3).Once a subplot is created, the axes can be titled using the
set_xlabel()command (orset_ylabel()).
Here are our three plots side by side:
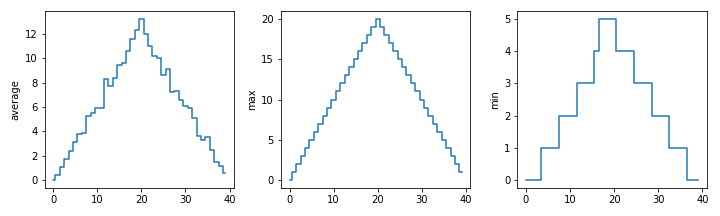
import numpy import matplotlib.pyplot data = numpy.loadtxt(fname='inflammation-01.csv', delimiter=',') fig = matplotlib.pyplot.figure(figsize=(10.0, 3.0)) axes1 = fig.add_subplot(1, 3, 1) axes2 = fig.add_subplot(1, 3, 2) axes3 = fig.add_subplot(1, 3, 3) axes1.set_ylabel('average') axes1.plot(numpy.mean(data, axis=0)) axes2.set_ylabel('max') axes2.plot(numpy.max(data, axis=0)) axes3.set_ylabel('min') axes3.plot(numpy.min(data, axis=0)) fig.tight_layout() matplotlib.pyplot.savefig('inflammation.png') matplotlib.pyplot.show()
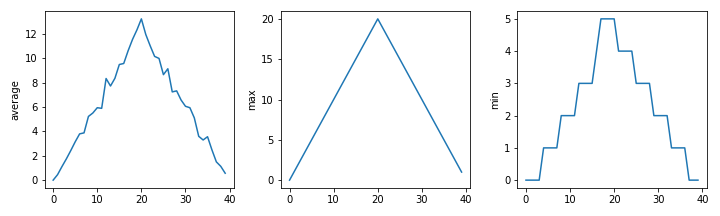
The call to loadtxt reads our data, and the rest of the program tells the plotting library how large we want the figure to be, that we're creating three subplots, what to draw for each one, and that we want a tight layout.
(If we leave out that call to fig.tight_layout(), the graphs will actually be squeezed together more closely.)
The call to savefig stores the plot as a graphics file. This can be
a convenient way to store your plots for use in other documents, web
pages etc. The graphics format is automatically determined by
Matplotlib from the file name ending we specify; here PNG from
'inflammation.png'. Matplotlib supports many different graphics
formats, including SVG, PDF, and JPEG.
Importing libraries with aliases
In this lesson we use the import matplotlib.pyplot syntax to import the pyplot module of matplotlib.
However, as we saw earlier, aliases such as import matplotlib.pyplot as plt are frequently used.
Importing pyplot this way means that after the initial import, rather than writing matplotlib.pyplot.plot(...), you can now write plt.plot(...).
Another common convention is to use the shortcut import numpy as np when importing the NumPy library.
We then can write np.loadtxt(...) instead of numpy.loadtxt(...), for example.
Some people prefer these shortcuts as it is quicker to type and results in shorter lines of code - especially for libraries with long names!
You will frequently see Python code online using a pyplot function with plt, or a NumPy function with np,
and it's because they've used this shortcut.
It makes no difference to the functionality of your code which approach you choose to take, but you must be consistent as if you use
import matplotlib.pyplot as plt then matplotlib.pyplot.plot(...) will not work.
You must use plt.plot(...) instead.
However, when working with other people it is important you agree on how libraries are imported.
Plot Scaling
Why do all of our plots stop just short of the upper end of our graph?
If we want to change this, we can use the set_ylim(min, max) method of each 'axes',
for example:
axes3.set_ylim(0,6)
Update your plotting code to automatically set a more appropriate scale.
(Hint: you can make use of the max and min methods to help.)
Drawing Straight Lines
In the center and right subplots above, we expect all lines to look like step functions because non-integer value are not realistic for the minimum and maximum values. However, you can see that the lines are not always vertical or horizontal, and in particular the step function in the subplot on the right looks slanted. Why is this?
Make Your Own Plot
Create a plot showing the standard deviation (numpy.std) of the inflammation data for each day across all patients.
Moving Plots Around
Modify the program to display the three plots on top of one another instead of side by side.